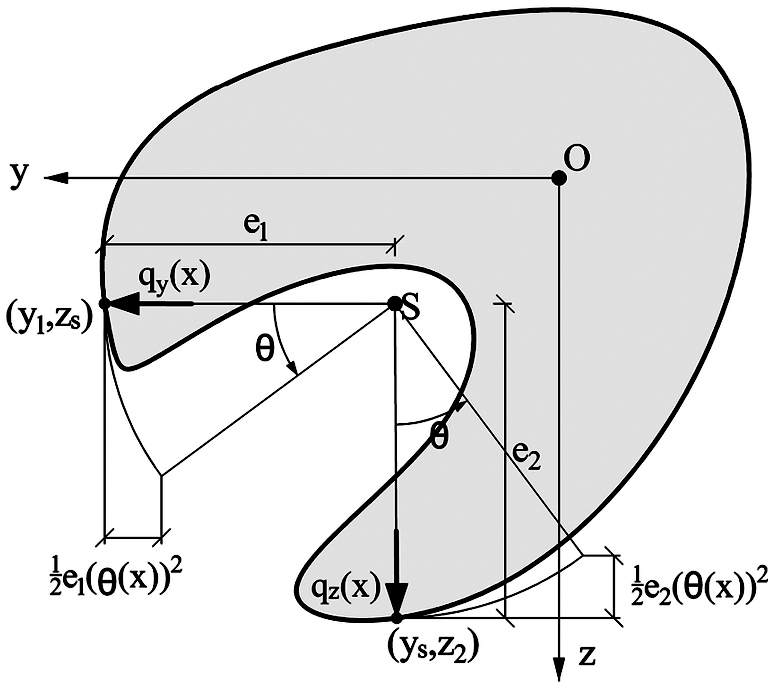
The paper deals with stability problems of straight elastic bars made of a homogenous isotropic material. The approach concerns both the bars of compact cross-sections and of thin-walled cross-sections, the transverse distortions being neglected. The stability analysis method developed for thin-walled bars in the paper: L. Zhang and G.S. Tong, “Flexural-torsional buckling of thin-walled beam members based on shell buckling theory”, Thin-Walled Structures, vol. 42(2004), pp. 1665–1687 is here extended to the bars whose deformations obey the assumptions of the Vlasov-like theory. The approach proposed makes it possible to assess the values of critical loads causing: axial forces, bending moments, transverse forces and torques, possibly simultaneously. The main task is to perform maximization of the relevant Rayleigh quotient; its form is given for all rational shapes of the bar’s cross section. The paper shows how to assess critical axial buckling loads and lateral buckling loads of straight elastic bars made of a homogenous isotropic material.