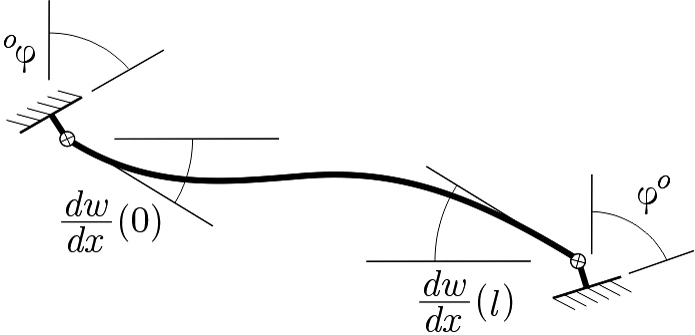
The classical theory of beams admits two types of connections between structural elements: perfectly rigid and perfectly flexible. However, the engineering reality calls for a more general approach to joint modelling. A non-ideal connection type is called semi-rigid. Its moment-rotation characteristic links the bending moment developed at the joint with the non-zero rotation increment between both sides of the connection. In the paper, the moment-rotation characteristic is assumed to be linearly elastic-perfectly plastic, and not sensitive to the sign of the rotation increment. Posed in the framework of Euler-Bernoulli’s theory of beams, the main objective of the paper is to formulate slope-deflection equations for a beam with semi-rigid joints. Two themes are considered. The first regards the equations derived under the assumption of small transverse displacements; the results are not new, but they offer a different viewpoint. The variational form of the equilibrium problem involves minimization of stress energy functional with constraints following from the yield condition imposed on the values of moments in semi-rigid joints. Such an approach furnishes a theoretical foundation for robust numerical analysis of large-scale frames in the full spectrum of joint deformation: linearly elastic and perfectly plastic. The second theme of study concerns the beam subjected to a large compressive force. The results obtained on the grounds of Bleich's linear theory of stability include slope-deflection equations and the implicit definition of the critical value of compressive force. In both themes of interest, the outcomes of the paper essentially extend the findings documented in the literature.